Dtjytyk

この項目「光円錐」は翻訳されたばかりのものです。不自然あるいは曖昧な表現などが含まれる可能性があり、このままでは読みづらいかもしれません。（原文：en:Light cone） 修正、加筆に協力し、現在の表現をより原文に近づけて下さる方を求めています。ノートページや履歴も参照してください。（2016年10月）

2＋1次元時空における光円錐。

特殊および一般相対性理論において、光円錐(こうえんすい 英: light cone) とはある事象（英語版） （時空上の一点）からあらゆる方向に向けて発せられた閃光が描く時空上の軌跡をいう。 ある二次元平面上に閉じ込められた光を考えてみれば、事象 E で発せられた光は同心円状に拡がっていき、時間を表わす縦軸を付け加えれば、光の軌跡は円錐を描くことがわかるだろう。これを未来光円錐と呼ぶ。過去光円錐とはこれを時間反転したもので、円の半径は光速で縮まっていき事象 E において一点に収縮する。実際には、空間の次元は3であるので、光は2次元平面上の円ではなく3次元空間上の球面を描いて拡がっていく4次元時空上の超円錐（英語版）（3次元空間上の円錐の断面が二次元平面上の円となるのと同様）であるが、この概念を可視化するためには空間次元を2に落としたほうが簡単である。

数式で表わせば座標 (x,y,z,t) が下記の式を満たす事象の集合である。

x2+y2+z2−(ct)2=0{displaystyle ,x^{2}+y^{2}+z^{2}-(ct)^{2}=0}

信号その他の因果関係の伝播は光速を超えることができないため（特殊相対性理論および量子もつれの項を参照のこと）、光円錐は因果律を定義する上で重要な役割を果たす。ある事象 E について、E の過去円錐内に含まれる事象群は信号を送って E に何らかの影響を与えることが可能である。例えば、E の十年前において E に将来影響を与えうるような事象をすべて集めると、 E が将来起こることになる位置を中心とする球体（2次元ならば円盤）を成す。したがって、この球面上およびその内側にある点は光速あるいはそれより遅い速度で伝播する信号を送り、事象 E に影響を及ぼすのに十分な時間があるということになる。逆に、その瞬間にこの球面の外側にある点は決して E に影響を及ぼすことはできない。同様に、事象 E の「未来」光円錐に含まれる事象は E の位置と時刻から信号を受け取ることができる全ての点を含むので、未来光円錐には E から相対論的因果律に従って影響を受ける可能性のある事象が全て含まれている。

数学的構成

特殊相対性理論において、光円錐（もしくはヌル円錐 英: null cone）はミンコフスキー時空上において閃光が時間発展する面を記述する。これを三次元空間上に可視化するためには、二つの水平軸を二つの空間次元に、一つの縦軸を時間にわりあてればよい^[1]。

光円錐は次のように構成できる。事象 p を時刻 t₀ における閃光（光パルス）とすると、この  p から発したパルスが到達できる全ての事象は p の未来光円錐を形成し、逆に p に光パルスを送ることのできる全ての事象がp の過去光円錐を形成する。

ある事象 E について、時空上の全ての事象は次の5つのカテゴリーに分けることができる。

• E の未来光円錐上にある事象


• E の過去光円錐上にある事象


• E の未来光円錐の内側にあり、E から発した物質粒子から影響を受け得る事象


• E の過去光円錐の内側にあり、そこから発した物質粒子が E で何が起こるかに影響を与え得る事象


• これ以外の全ての事象は E の（絶対） 他所 (elsewhere)^{[訳語疑問点]} にあり、E の影響を受けることも E に影響を与えることも不可能である。

上の分類はどのような基準系を用いても変わらない。つまり、ある観測者がある事象を光円錐の内側にあると判断したならば、他の全ての観測者から見ても、基準系に関わらず同じ光円錐の内側にあるということである。これがこの概念の強力さの理由である。

ここまでは特定の位置と特定の時刻に起こる事象について述べてきた。ある事象がもう一つの事象に影響を及ぼすことができないということは、光がある位置から別の位置に「与えられた時間内に」到達することができないということである。それらの事象から発する光は究極的には別の事象の「以前の」位置には到達するが、それがその事象が起こってしまった「後」になるということである。

時間が進むにつれ、ある事象の未来光円錐はより多くの位置を囲むことになる（言い換えれば、4次元時空上の光円錐のある時刻における断面である3次元空間上の球面は、時刻が後になるにつれて大きくなる）。同様に、ある事象から時間を遡ることを考えると、その事象の過去光円錐は未来光円錐と同じように時間が遡るにつれてより多くの事象を囲むことになる。より遠い位置は当然より時間が経ってからになる。今日の地球で起こる事象の過去光円錐を例にとれば、一万光年離れた星は一万年以上遡らなければ光円錐の中に含まれない。 今日の地球で起こるある事象の過去光円錐は、その端の方では非常に遠い物体をも（可観測宇宙に存在する全てをも）含むことになるが、非常に昔、宇宙が若かったころの姿を見ることになる。

異る場所で（ある基準系で）同じ時刻に起こる二つの事象は常に相手の過去光円錐にも未来光円錐にも含まれない。光は瞬時に伝わることはできないからである。もちろん、他の観測者にはこれら二つの事象が別の時刻、別の場所で起こるように見えるだろうが、どちらにせよどちらの光円錐にも入らないことは同じなのである。

真空中の光速を1とするような単位系を使えば、例えば距離の単位を光秒とし時間の単位を秒とすれば、光は1秒のうちに真空中を1光秒だけ進むので、光円錐の傾きは 45° となる。特殊相対性理論においては光速は全ての慣性系において不変であるから、全ての観測者の光円錐は同じく 45° の傾きを持つ。ローレンツ変換の性質を表すには一般的にミンコフスキーダイアグラム（英語版）が用いられる。ある事象の光円錐の外側の、一繋がりの部分を他所 (elsewhere)^{[訳語疑問点]} と呼ぶ。互いに他所の関係にある事象は相互に観測不可能であり、因果律的に繋がることはできない。

(45° という数字は空間的な意味しか持たない。実際の時空の性質を理解するために空間に引き落して図を書いているためである。空間的な傾きは角度で測られ、三角関数で計算される。これに対して、時空的な傾きはラピディティによって測られ、双曲線関数により計算される。）

一般相対性理論における光円錐

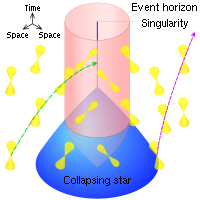
重力崩壊を起こし星がブラックホールとなる瞬間の近傍における光円錐。紫色の破線は重力崩壊しつつある星の表面から発せられる光の軌跡を示す。緑色の一点鎖線は特異点へと落ちる光の軌跡を示す。

平坦な時空においては、ある事象の未来光円錐はその因果的未来（英語版）の境界であり、 過去光円錐はその因果的過去（英語版）のの境界である。

曲がった時空では、大域双曲時空（英語版）を仮定した場合はある事象の未来光円錐がその因果的未来の境界を含むことまでは成り立つ（過去も同様）。しかし、重力レンズ効果により光円錐の一部が自身の内側に折り込まれ、光円錐の一部が因果的未来（もしくは過去）の境界ではなくその厳密な内側となることもありうる。

また、全ての光円錐が平行な傾きを持つことはなくなる。このことは時空が曲がっておりミンコフスキー空間とは本質的に異なっていることを反映している。真空領域中（物質の存在しない時空領域）においては、全ての光円錐が平行でないことはワイルテンソル（英語版）が非零となることを意味する。

関連項目

• 絶対未来（英語版）


• 絶対過去（英語版）


• 双曲型偏微分方程式


• 光円錐座標


• ローレンツ変換


• 特性曲線法


• ミンコフスキーダイアグラム（英語版）


• モンジュ円錐（英語版）


• ヌル円錐（英語版）


• 波動方程式

出典

外部リンク

• The Einstein-Minkowski Spacetime: Introducing the Light Cone
  


• The Paradox of Special Relativity


• RSS feed of stars in one's personal light cone

表 話 編 歴 相対性理論 特殊 相対論 背景 相対性原理 特殊相対性理論 基礎 相対運動 基準系 光速 マクスウェルの方程式 公式 ガリレイ相対性（英語版） ガリレイ変換 ローレンツ変換 結果 時間の遅れ 相対論的質量（英語版） E = mc2 長さの短縮（英語版） 同時性の相対性（英語版） 相対論的ドップラー効果（英語版） トーマス歳差（英語版） 相対論的ディスク（英語版） 時空 ミンコフスキー時空 世界線 ミンコフスキーダイアグラム（英語版） 光円錐 一般 相対論 背景 一般相対論の数学 関連文献 基礎 特殊相対性理論 等価原理 世界線 リーマン幾何学 ミンコフスキーダイアグラム（英語版） 現象 二体問題（英語版） 重力レンズ 重力波 慣性系の引きずり 測地的効果（英語版） 事象の地平面 重力の特異点 ブラックホール 方程式 線形化重力（英語版） PPN形式 アインシュタイン方程式 測地線 フリードマン方程式 ADM形式（英語版） BSSN形式（英語版） ハミルトン＝ヤコビ＝アインシュタイン方程式（英語版） 発展 理論 カルツァ＝クライン理論 量子重力理論 ブランス＝ディッケ理論（英語版） 解（英語版） シュワルツシルト ノルドシュトロム ゲーデル カー カー・ニューマン カスナー（英語版） タアブ・NUT（英語版） ミルン（英語版） フリードマン・ルメートル・ロバートソン・ウォーカー pp-wave時空（英語版） ファン・ストックム・ダスト（英語版） 科学者 アインシュタイン ローレンツ ヒルベルト ポアンカレ シュヴァルツシルト ド・ジッター ライスナー ノルドシュトルム ワイル エディントン フリードマン ミルン ツビッキー ルメートル ゲーデル ホイーラー ロバートソン バーディーン ウォーカー カー チャンドラセカール エーラス（英語版） ペンローズ ホーキング テイラー ハルス ストックム（英語版） タアブ（英語版） ニューマン（英語版） ヤウ ソーン ノッターレ（英語版） その他（英語版）