Dtjytyk

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。（2011年7月）

ローレンツ変換（ローレンツへんかん、英: Lorentz transformation）は、2 つの慣性系の間の座標（時間座標と空間座標）を結びつける線形変換で、電磁気学と古典力学間の矛盾を回避するために、アイルランドのジョセフ・ラーモア（1897年）とオランダのヘンドリック・ローレンツ（1899年、1904年）により提案された。

アルベルト・アインシュタインが特殊相対性理論（1905年）を構築したときには、慣性系間に許される変換公式として、理論の基礎を形成した。特殊相対性理論では全ての慣性系は同等なので、物理法則はローレンツ変換に対して不変な形、すなわち同じ変換性をもつ量の間のテンソル方程式として与えられなければならない。このことをローレンツ不変性(共変性)をもつという。

幾何学的には、ミンコフスキー空間における 2 点間の世界間隔を不変に保つような、原点を中心にした回転変換を表す（ミンコフスキー空間でみたローレンツ変換節参照）。

概要

ローレンツ変換は、マイケルソン・モーリーの実験結果を矛盾なく説明する手段として提案された。ローレンツは、時間の流れや光速度はすべての基準座標系において同一と考えたため、「大きな速度で動く座標系では、2 点間の距離（物体の長さ）は縮む」というローレンツ収縮を結論した。しかし、ローレンツ収縮は実験結果と矛盾した。後に、アインシュタインは、光速度の不変性と物理法則の相対性（「物理法則はあらゆる慣性系間で同一である」）の 2 つを原理として、特殊相対性理論を築いた。そこでは、ローレンツ変換から帰結される事実として、時間の進み方が観測者によって異なることを結論した。

ガリレイ変換は、等速運動をする慣性系間の座標変換であり、ニュートンの運動方程式は不変な形で変化するが、マクスウェルの方程式では満足されない古典的な座標変換である。ローレンツ変換は、マクスウェル方程式を不変な形で変換する。また慣性系の動く速度 v が、光速度 c に比べて十分小さい場合（v/c → 0 と見なせる場合）を考えると、ローレンツ変換はガリレイ変換を再現する。したがって、非相対論的な極限でガリレイ不変性が成立しているという事実もローレンツ変換で説明できる。

ローレンツ変換のうち、空間と時間が関与する方向への変換をローレンツブースト (英: Lorentz boost) と呼ぶ。特殊相対論が導く、我々の直感に反する事柄のほとんどは、このローレンツブーストからの帰結である。一方で、空間同士が関与する変換はただの空間回転である。

物理的導入

ローレンツ変換は、ある慣性系 S における空間および時間座標（あるいは任意の 4元ベクトル）を、x-軸に沿った S に対する相対速度 v で移動する別の慣性系 S′ へ変換する際に使用される群作用である。原点 (0, 0, 0, 0) を共有する、S における時空座標 (t, x, y, z) と S′ における時空座標 (t′, x′, y′, z′) で記述される事象の座標系は、以下のローレンツ変換によって関連づけられる。

上式で

はローレンツ因子と呼ばれ、c は真空中の光速度を表す。

行列での表現

上の 4 つの方程式は、行列を用いて表現できる。

あるいは、以下のようにも記述できる。

最初の式は、v/c → 0 となる極限において、ガリレイ変換に帰着することを容易に理解できる点で、第 2 の式は、相対論における基本的な不変量である時空間隔 ds² = (cdt)² − dx² − dy² − dz² が保存されることを容易に理解できる点で、それぞれ優れている。

ミンコフスキー空間でみたローレンツ変換

また、パラメータ θ を用いて、

vc=tanh⁡θ{displaystyle {frac {v}{c}}=tanh theta }

とすると

ct′=ctcosh⁡θ−xsinh⁡θx′=xcosh⁡θ−ctsinh⁡θ{displaystyle {begin{aligned}ct'&=ctcosh {theta }-xsinh {theta }\x'&=xcosh {theta }-ctsinh {theta }end{aligned}}}

虚時間 w = i ct を用いれば、

w′=wcos⁡iθ−xsin⁡iθx′=xcos⁡iθ+wsin⁡iθ{displaystyle {begin{aligned}w'&=wcos {itheta }-xsin {itheta }\x'&=xcos {itheta }+wsin {itheta }end{aligned}}}

行列を用いれば、それぞれ

と表すことができる。この表現を用いると、ローレンツ変換がミンコフスキー空間上での虚数角 iθ の回転に相当することが容易に理解できる。

この表式では速度の合成が容易になる。慣性系 S において、速度 u で x-軸方向に等速運動している物体は、慣性系 S′ における速度 u′ は、

uc=tanh⁡ϕ{displaystyle {frac {u}{c}}=tanh {phi }}

とすると、

u′c=tanh⁡(ϕ−θ){displaystyle {frac {u'}{c}}=tanh {(phi -theta )}}

で表される。

相対速度 v の方向が 慣性系 S の x-軸方向と一致する場合にのみ、上の方程式は適用される。v の方向が S の x-軸と一致しない場合には、ローレンツ変換の一般解を求めるよりも、v の方向が S の x-軸と一致するように慣性系の回転を行うほうが、一般に容易である。

空間ベクトルの分解

任意の方向へのローレンツブーストに際しては、空間ベクトル x を速度 v と平行な垂直成分に x=x⊥+x‖{displaystyle {boldsymbol {x}}={boldsymbol {x}}_{perp }+{boldsymbol {x}}_{|}} と分解すると都合が良い。v 方向の成分 x‖{displaystyle {boldsymbol {x}}_{|}} のみが、ローレンツ因子 γ による変形を受ける。

上の方程式は、行列を用いて以下のように表現できる。

ここで、v^T は v の転置行列、I は 3 次単位行列である。

上で注記したように、この変換は 2 つの系で原点が共有されることを要求する。この制約を緩和する形で、ローレンツ変換に時空の平行移動を加えた変換はポアンカレ変換と呼ばれる。

より一般的な定義

なお、ローレンツ変換は「光速度一定」の帰結である「世界間隔の不変性」を満たす変換として、より一般的に定義される。ここで、時空を記述する 4元ベクトル x=(ct , x, y, z ) に対し、

ΛTgΛ=g{displaystyle Lambda ^{mathrm {T} }gLambda =g,}

を満たす任意の 4×4 行列 Λ によって与えられる変換

x→x′=Λx{displaystyle xrightarrow x'=Lambda x}

がローレンツ変換となる。但し、T は転置行列を表し、g は

で与えられる時空の計量テンソルを表すものとする。

このように定義された行列 Λ の全体は、ローレンツ群として知られる群 SO(3,1) を構成する。

厳密に言うと、このように定義したローレンツ変換はミンコフスキー空間での回転だけでなく、空間反転に相当するパリティ変換 P、時間反転 T を含む。これらの変換は連続的なローレンツ変換とは別個に扱われる場合が多い。例えば実際の物理は連続的なローレンツ変換に対しては不変だが、パリティ対称性の破れ、CP対称性の破れ（CPT定理より T の破れと同義）は実験で観測されている。この点を明確にしたい場合、連続的な回転のみの部分を本義ローレンツ変換と呼ぶことがある。

一般的ローレンツ変換

定義

より一般的に、ローレンツ変換は世界間隔を不変に保つ線形変換として定義される。こうして定義されるローレンツ変換は、ミンコフスキー時空における内積に対する対称性として捉えることができる。
まず、ミンコフスキー時空におけるローレンツ変換 Λ は

ΛTgΛ=g{displaystyle Lambda ^{mathrm {T} }gLambda =g}

すなわち

ΛλμgλρΛρν=gμν(μ,λ,ρ,ν=0,1,2,3){displaystyle {Lambda ^{lambda }}_{mu }g_{lambda rho }{Lambda ^{rho }}_{nu }=g_{mu nu }quad (mu ,lambda ,rho ,nu =0,1,2,3)}

を満たす線形変換として定義される。但し、g =(g_μν) は、g =diag(1, −1, −1, −1) で与えられる計量テンソルであり、重複する添え字に対してはアインシュタインの縮約に従って和をとるものとする。また、添え字の上げ下げは計量テンソルによって、

xμ=gμνxν{displaystyle x_{mu }=g_{mu nu }x^{nu }}

で、与えられるものとする。

性質

こうして定義されるローレンツ変換は、時空の二点 x =(x⁰, x¹, x², x³)、y =(y⁰, y¹, y², x³)のローレンツ内積

x⋅y=xμyμ=x0y0−x1y1−x2y2−x3y3{displaystyle xcdot y=x^{mu }y_{mu }=x^{0}y^{0}-x^{1}y^{1}-x^{2}y^{2}-x^{3}y^{3}}

を不変に保つ。

x′⋅y′=x⋅y(x′=Λx,y′=Λy){displaystyle x'cdot y'=xcdot yquad (x'=Lambda x,y'=Lambda y)}

この性質から、特に時空の計量

ds2=gμνdxμdxν=(dx0)2−(dx1)2−(dx3)2−(dx3)2{displaystyle mathrm {d} s^{2}=g_{mu nu }mathrm {d} x^{mu }mathrm {d} x^{nu }=(mathrm {d} x^{0})^{,2}-(mathrm {d} x^{1})^{,2}-(mathrm {d} x^{3})^{,2}-(mathrm {d} x^{3})^{,2}}

はローレンツ変換の下、不変となる。

ds′2=ΛλμgλρΛνρdxμdxν=ds2{displaystyle mathrm {d} s'^{2}=Lambda _{,,lambda }^{mu }g_{lambda rho }Lambda _{,,nu }^{rho }mathrm {d} x^{mu }mathrm {d} x^{nu }=mathrm {d} s^{,2}}

すなわち、世界間隔は不変に保たれる。

ローレンツ変換の分類

ローレンツ変換全体のなす集合 L は、行列式と00成分 Λ⁰⁰ によって分類される。ローレンツ変換 Λ において、その行列式 det(Λ) は ±1 の値をとる。一方、 00成分は Λ⁰⁰ ≥1 または Λ⁰⁰ ≤−1 を満たす。ローレンツ変換の全体 L の中で、行列式の値と00成分の符号が等しい2つのローレンツ変換は、連続的に移り変わることができる連結な成分となる。一方、これらが異なる2つのローレンツ変換は連続的に移り変わることができない非連結な成分となる。従って、L は行列式の値並びに00成分の符号によって、次の4つの連結な部分集合に分類される。

L+↑:={Λ∈L|detΛ=+1,Λ00≥+1}L−↑:={Λ∈L|detΛ=−1,Λ00≤−1}L+↓:={Λ∈L|detΛ=+1,Λ00≥+1}L−↓:={Λ∈L|detΛ=−1,Λ00≤−1}{displaystyle {begin{aligned}L_{+}^{uparrow }&:={Lambda in L|det {Lambda }=+1,Lambda _{,,0}^{0}geq +1}\L_{-}^{uparrow }&:={Lambda in L|det {Lambda }=-1,Lambda _{,,0}^{0}leq -1}\L_{+}^{downarrow }&:={Lambda in L|det {Lambda }=+1,Lambda _{,,0}^{0}geq +1}\L_{-}^{downarrow }&:={Lambda in L|det {Lambda }=-1,Lambda _{,,0}^{0}leq -1}end{aligned}}}

この分類において、Λ⁰₀ ≥1 を満たすものを順時間的（orthochrous）、Λ⁰₀ ≤−1 を満たすものを反順時間的（anti-orthochrous）、det(Λ )=1を満たすものを固有（proper）、det(Λ )=−1 を満たすものを非固有（improper）と呼ぶ。

ローレンツ変換の中で、特別なものとして、

(Ix)μ=xμ(μ=0,1,2,3)(Px)0=x0(Px)i=−xi(i=1,2,3)(Tx)0=−x0(Tx)i=xi(i=1,2,3)(PTx)μ=(P∘Tx)μ=−xμ(μ=0,1,2,3){displaystyle {begin{aligned}(Ix)^{mu }&=x^{mu }quad (mu =0,1,2,3)\(Px)^{0}&=x^{0}quad (Px)^{i}=-x^{i}quad (i=1,2,3)\(Tx)^{0}&=-x^{0}quad (Tx)^{i}=x^{i}quad (i=1,2,3)\(PTx)^{mu }&=(Pcirc Tx)^{mu }=-x^{mu }quad (mu =0,1,2,3)end{aligned}}}

で定義される恒等変換 I、空間反転（パリティ変換） P、時間反転 T、空間時間反転 PT が存在する。

L^↑₊, L^↑₋, L^↓₊, L^↓₋ はそれぞれ、恒等変換 I 、空間反転 P、時間反転 T、空間時間反転 PT を含む。

I∈L+↑,P∈L−↑,T∈L+↓,PT∈L−↓{displaystyle Iin L_{+}^{uparrow },,,Pin L_{-}^{uparrow },,,Tin L_{+}^{downarrow },,,PTin L_{-}^{downarrow }}

これらの変換により、L^↑₊, L^↑₋, L^↓₊, L^↓₋ は次のように結び付けられる。

L+↑=PL−↑L+↑=TL−↓L+↑=PTL+↓{displaystyle {begin{aligned}L_{+}^{uparrow }&=PL_{-}^{uparrow }\L_{+}^{uparrow }&=TL_{-}^{downarrow }\L_{+}^{uparrow }&=PTL_{+}^{downarrow }end{aligned}}}

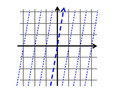
図

慣性系 S と慣性系 S′ の座標格子を重ねて図示すると、ローレンツ変換とガリレイ変換の違いがイメージできる。ガリレイ変換では時刻が等しい点からなる直線（同時刻線）は両慣性系で一致するが、ローレンツ変換では異なる慣性系の同時刻線は互いに傾いている。これはローレンツ変換では、慣性系 S では同時に起きた事象が慣性系 S′ では異なる時刻に起きていることを意味する。これを同時性の崩れという。

• 
  

  

  
  

  
  

  座標格子のローレンツ変換
  

  
  

  
  


• 
  

  

  
  

  
  

  座標格子のガリレイ変換
  

  
  

  
  

歴史

ローレンツはこの変換がマクスウェル方程式を不変な形で変換することを、1900年に発見した。ローレンツは導光性エーテル仮説を信じており、この変換に適切な基礎を提供する相対性理論を発見したのは、アルベルト・アインシュタインであった。

ローレンツ変換は1904年に初めて発表されたが、当時これらの方程式は不完全であった。フランスの数学者アンリ・ポアンカレが、ローレンツの方程式を、今日知られている整合性の取れた 4 つの方程式に修正した。

ローレンツ＝フィッツジェラルド収縮

ローレンツの解釈

この節の加筆が望まれています。

相対論的解釈

ローレンツ収縮

アインシュタインの解釈によれば、観測者に対して運動する物体は縮んで観測される。

例として、x-軸方向に長さを持つ物体が、観測者 A （xyzw-座標系）に対して x-軸正方向に速度 v で等速直線運動する場合を考える (w = ct)。この物体と共に運動する観測者 B （x′y′z′w′-座標系）にはこの物体の長さが l で観測されるとする(w′ = ct′)。これはすなわち、観測者 B にとって同時刻に観測したときに、物体の端と端の x′-座標の値の差が l であることを示す。

t′ = 0 のとき、物体の片端が x′ = 0、もう一方の端が x′ = l にあるとする。このとき、物体の軌跡は {(x′, w′) | 0 ≤ x′ ≤ l} となり、右図薄青部である。ここで、β=vc,γ=11−β2{displaystyle beta ={frac {v}{c}},gamma ={frac {1}{sqrt {1-beta ^{2}}}}}とおくと、x′ = γ(x − βw) であるため、0≤x′≤l⟺βw≤x≤βw+lγ{displaystyle 0leq x'leq liff beta wleq xleq beta w+{frac {l}{gamma }}} となる。すなわち、t = 0 のとき、片端は x = 0 に、もう片端は x=lγ{displaystyle x={frac {l}{gamma }}} にあるので、観測者 A にとってこの物体の長さは lγ{displaystyle {frac {l}{gamma }}} となることが分かる（なお、観測者 A にとって (x, w) = (0, l) となる点は、右図点線である双曲線 x² − w² = l と x-軸の交点であることからもローレンツ収縮の影響がわかる）。

関連項目

• ヘンドリック・ローレンツ


• 特殊相対性理論


• 電磁気学


• マクスウェル方程式


• 一般相対性原理


• ガレージのパラドックス


• ガリレイ変換


• ウィック回転

表 話 編 歴 相対性理論 特殊 相対論 背景 相対性原理 特殊相対性理論 基礎 相対運動 基準系 光速 マクスウェルの方程式 公式 ガリレイ相対性（英語版） ガリレイ変換 ローレンツ変換 結果 時間の遅れ 相対論的質量（英語版） E = mc2 長さの短縮（英語版） 同時性の相対性（英語版） 相対論的ドップラー効果（英語版） トーマス歳差（英語版） 相対論的ディスク（英語版） 時空 ミンコフスキー時空 世界線 ミンコフスキーダイアグラム（英語版） 光円錐 一般 相対論 背景 一般相対論の数学 関連文献 基礎 特殊相対性理論 等価原理 世界線 リーマン幾何学 ミンコフスキーダイアグラム（英語版） 現象 二体問題（英語版） 重力レンズ 重力波 慣性系の引きずり 測地的効果（英語版） 事象の地平面 重力の特異点 ブラックホール 方程式 線形化重力（英語版） PPN形式 アインシュタイン方程式 測地線 フリードマン方程式 ADM形式（英語版） BSSN形式（英語版） ハミルトン＝ヤコビ＝アインシュタイン方程式（英語版） 発展 理論 カルツァ＝クライン理論 量子重力理論 ブランス＝ディッケ理論（英語版） 解（英語版） シュワルツシルト ノルドシュトロム ゲーデル カー カー・ニューマン カスナー（英語版） タアブ・NUT（英語版） ミルン（英語版） フリードマン・ルメートル・ロバートソン・ウォーカー pp-wave時空（英語版） ファン・ストックム・ダスト（英語版） 科学者 アインシュタイン ローレンツ ヒルベルト ポアンカレ シュヴァルツシルト ド・ジッター ライスナー ノルドシュトルム ワイル エディントン フリードマン ミルン ツビッキー ルメートル ゲーデル ホイーラー ロバートソン バーディーン ウォーカー カー チャンドラセカール エーラス（英語版） ペンローズ ホーキング テイラー ハルス ストックム（英語版） タアブ（英語版） ニューマン（英語版） ヤウ ソーン ノッターレ（英語版） その他（英語版）