Transformator

Fig. 1 Døme på små effekttransformatorar.
Transformator er ein elektomagnetisk komponent som vert nytta for impedansetransformasjon, som tilsvarar at spenninga eller straumen vert transformert opp eller ned. Om spenninga vert transformert opp vert straumen transformert ned, eller motsett.
Innhaldsliste
1 Grunnleggande oppbygging og verkemåte
1.1 Ideell transformator
2 Ulike typar transfomatorar
2.1 Effekttransformatorar
2.2 Signaltransformatorar
Grunnleggande oppbygging og verkemåte |
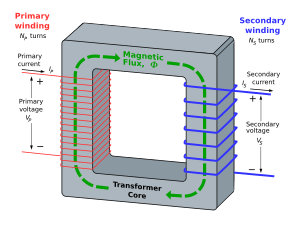
Fig. 2 Transformator.
Transformatorar er bygd opp med to galvanisk isolerte krinsar som er kopla saman med ein magnetisk fluks. Dei to krinsane, som vert kalla primærkrins og sekundærkrins, har kvar sin spole som er vikla rundt eit materiale med liten reluktans (kalla transformatorkjernen), som den magnetiske fluksen fylgjer, Fig. 2.
Fluksen i den magnetiske krinsen
- ϕ=N1iR,displaystyle phi =frac N_1imathfrak R,
der N1 er vinningstalet i primærspolen, i er straumen i primærspolen og Rdisplaystyle mathfrak R er reluktansen til transformatorkjernen. Fluksen fylgjer den magnetiske leiaren (transformatorkjernen), slik at same fluksen går gjennom begge spolane. I sekundærkrinsen induserer fluksen (i fylgje Faradys lov) ei spenning
- v2=N2dΦdt,displaystyle v_2=N_2frac mathrm d Phi mathrm d t,
der N2 er vinningstalet i sekundærviklinga og dΦdtdisplaystyle frac mathrm d Phi mathrm d t er den tidsderiverte av fluksen. Forholdet mellom spenningane i sekundær- og primærkrinsen kan difor uttrykkast
- v2v1=N2N1.displaystyle frac v_2v_1=frac N_2N_1.
Ideell transformator |
Ein ideell transformator er ein forenkla modell av ein transformator som ikkje har tap. Fig. 3 syner ein ideell transformator med ein lastimpedans ZLdisplaystyle Z_L i sekundærkrinsen. Straumen i lastmotstanden
- i2=V2ZL.displaystyle i_2=frac V_2Z_L.
Ein ideell transformator har ikkje tap, så effekten i sekundærkrinsen må vera lik effekten i primærkrinsen:
- P1=P2,displaystyle P_1=P_2,
som er det same som at
- v1i1=v2i2.displaystyle v_1i_1=v_2i_2.
Ved å kombinera likningane kjem ein fram til fylgjande samanhengar for ein ideell transformator:
- v2v1=i1i2=N2N1.displaystyle frac v_2v_1=frac i_1i_2=frac N_2N_1.
Om N2>N1displaystyle N_2>N_1 vert spenninga transformert opp (v2>v1displaystyle v_2>v_1) og straumen vert transformert ned (i2>i1displaystyle i_2>i_1).
Lastimpedansen sett frå primærsida kan uttrykkast
- ZL′=v1i1=v2(N1N2)i2(N2N1)=(v2i2)(N1N2)2=ZL(N1N2)2.displaystyle Z_L'=frac v_1i_1=frac v_2left(!frac N_1N_2right)i_2left(!frac N_2N_1right)=left(!frac v_2i_2right)!left(!frac N_1N_2right)^2=Z_L!left(!frac N_1N_2right)^2.
På same måte kan kildeimpedanse Zkdisplaystyle Z_k sett frå sekundærsida uttrykkast
- Zk′=Zk(N2N1)2.displaystyle Z_k^'=Z_k!left(!frac N_2N_1right)^2.
Ein ser at spenningar og straumar vert transformerte med omsettingsforholdet N2N1displaystyle frac N_2N_1, medan impedansar vert transformerte med kvadratet av omsetningsforholdet.
Ulike typar transfomatorar |
Effekttransformatorar |
Signaltransformatorar |
Elektrofag | |
|---|---|
| Generelt | Elektromagnetisme · Elektroteknikk · Elektriske målingar |
| Elektronikk | Elektronikk · Telekommunikasjon · Signalhandsaming · Elektromagnetisk kompatibilitet · Optoelektronikk · Interfacing · Reguleringsteknikk · Mekatronikk · Kraftelektronikk · Eletroniske måleinstrument |
| Elkraft | Elektrisk generator · Elektrisk motor · Transformator · Elnett · Kraftelektronikk |
|
















